How to overcome maths issues and learn to excel at maths
Answering a question on Quora has prompted me to put this page together, based on challenges I and others have faced in learning maths at different levels.
Can I ask you to start by REALISTICALLY grading your attitude / feeling about maths?
- "I cant understand any math at all."
- "I hate it, I'm not good at math";
- "I'm OK but struggling with some parts";
- "Doing alright but its slow";
- "I love math, its my best subject".
If you fit into categories 1 or 2 you may have a break in your understanding - so after the introduction that follows first see section 1.
If you fit into category 3 it may be that a lack of confidence is hampering the speed at which you make progress. You may still benefit from going back over early ideas so check out section 1 anyway.
Whether you fit into categories 3 or 4 you will find following the ideas in section 2 will help you become MUCH better at math.
And what about category zero? If that is a genuine reflection of your ability - not your attitude - then see the last section on Dyscalculia. Otherwise carry on here.
Introduction: Maths is not "hard".
Maths is basically a series of steps that you climb. The steps aren't all the same height - but you CAN go up them. However unlike most other subjects each stage is very dependent on the earlier stages - so an early weakness can have a very major effect.
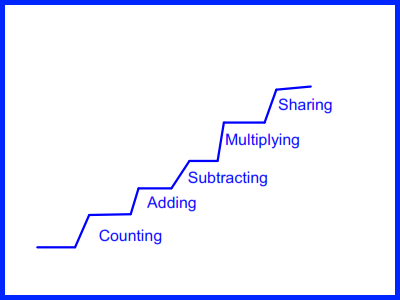
Primary School maths
This diagram illustrates our progress in early (pre-school) math. These stages will all use physical representations of numbers, such as "compare bears" or dots on a die or dominoes. So counting will be counting real items. The math operators (+,-, * etc) will be introduced but problems such as 2*3 will be treated as two groups of three items. Each new idea is based on concepts already learnt. Generally you cant go on to the next until you are competent at the earlier levels. People with dyscalculia (see below) often run into difficulties at this stage. The pattern of progression in further maths is similar.
Maths beyond primary school and on to university
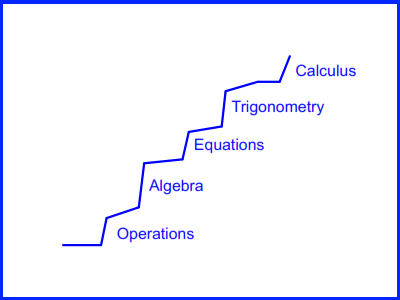
School maths
This diagram - a great oversimplification - shows some stages of progress in more advanced math. Again each new idea is based on concepts already learnt. The curriculum and sequence may vary but many of the "steps" still take place. We learnt in early years that a number "3" can represent three cars or three sheep. Here we start with "operations" - the basic operations we learnt at primary school - addition, subtraction, etc.; but now with numbers as abstractions rather than physical items. Then add new ones - squares, cubes, roots, factorials etc. People with dyscalculia will generally find this step insuperable.
Then algebra, where the notion of representing numbers as letters may cause some difficulties. Equations solved by algebra with different methods such as factorisation.
Trigonometry introduces new functions that at first seem to have little importance in our experience of the real world, but is a hugely important foundation for math beyond that level;
Then Calculus, again introducing new notation and new ways of working.
There are also other "threads" such as statistics - but again building on work you are assumed to already understand.
Section 1: If you are having some difficulty: Why do some people find maths "hard"?
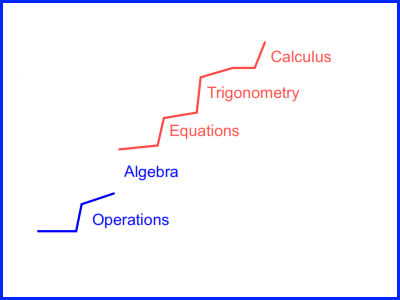
A break in your understanding
This diagram shows what happens if you are missing some important foundation work. You continue to attend lessons, and struggle to solve problems. All the succeeding stages are built on a shaky foundation, and you will never be fully confident unless the gap in your knowledge is addressed. Lets take an example from my own life. At school, due to a long illness, I missed the early work on trigonometry. On my return I struggled on but my previously good grades deteriorated. I enjoyed the early work on calculus - which is basically built on algebra and operations; but as soon a it progressed to handling trigonometric functions I was totally lost.
Additional study and remedial work did not help - the basics just were not there so there was no way I could understand it.
It was only years later, when I attended a "basic" math course, that I learnt about Sin, Cos & Tan - and the rest all suddenly started to make sense.
How do these difficulties arise?
If you are having difficulty you need to analyse where that difficulty starts. It may not be obvious. Suppose you are finding algebra difficult. It likely is because the idea of using letters to represent numbers - constants and variables - isnt familiar. However it may be because you have a previously unnoticed difficulty that you have developed strategies to cope with, but these strategies no longer work with algebra.
Heres an example. Sally is very good at successive addition - so she never learns multiplication tables. In early school she does well at math, but for every multiplication she has to do the addition; She learns coping strategies - so 7*3 = 7+7+7 and 3*7 = 7+7+7, reducing the number of additions. Then more demanding problems arise - such as 257 * 396; and long division; and algebra. Her strength has become a weakness.
How can I find the problem?
You MAY be able to narrow it down yourself to a particular area. Perhaps you are aware that you are better at some particular parts of the syllabus. However the problem may also be deep rooted as in "Sally"s case, and more difficult to track down. Importantly you may have become dispirited, feel that you "just arent good at math" and intimidated by math problems. This negative atttitude will itself harm your progress.
Perhaps the best response is to sit down with an independent tutor who can help you find and resolve your weaknesses. Its best if this is not a teacher from your school, as they can feel responsible or being blamed. You need a different viewpoint. Once you have found your weak spots you will need to do some (limited) remedial work to strengthen the work that built on those weak foundations.
You also need to realise that your issues with math are not your fault, you aren't "bad at math" and you can do dramatically better once your underlying weakness has been fixed.
Section 2: How to become DRAMATICALLY better at Maths.
How did I learn this "secret"?
In my final degree math exam (3 hours, answer 4 from 6) I left after 90 minutes, having answered all six questions, and checked the answers. I scored 98%.
How was I able to do this? For two years I had been in a class where the tutor introduced a topic, and gave us 40 examples to answer. We could leave when we finished; and if I left early I could catch a bus otherwise I'd have a long wait. The habit of working quickly and trusting my working never left me. I owe that tutor (and the bus company) a lot.
Here is the secret. Solving multiple problems under time pressure taught me:
- to focus and not be distracted
- to work quickly and
- to trust my working
Having confidence meant I could move straight on to the next problem. You can do just as well. Your best friend is a ticking timer.
FIRST: DONT PRACTISE MISTAKES.
Do an example problem, and check your answer so you know you are using the right procedure. If you make a mistake, analyse where the error is, then do another problem.
SECOND: WORK UNDER TIME PRESSURE.
Then set the timer for 40 minutes, and answer as many questions as you can. Or if you have two different types of problem, allow 20 minutes for each, with a short break between. STOP when the time has elapsed. At first this is very tiring but you will soon get used to it.
THEN:
Have a reward, take a short break, check your answers, then write down what you have learnt, with an example.
Prepare, record and review
Ask for a study plan so you know what topics are coming next, then you can do a little preparation ahead of your class; keep a note of topics you have covered and record any new processes you have been taught - a single example is often enough as a reminder. You can use this record to prepare for exams and also to guide your reviews. There's more information on breaks and rewards, study skills and reviewing on this page.
3: Dyscalculia
This is a is a learning difference that causes trouble with maths. Its not a "weakness", true dyscalculia is an inability to perform some math operations. Typically someone with dyscalculia may be able to count and add, but be unable to understand the difference between math operations such as addition and subtraction. Its easily diagnosed, but there is no cure, and learning support involves developing coping strategies. Its usually VERY apparent, and noticed long before you reach secondary school. More information here: About Dyscalculia
